Spontaneous wave formation in stochastic self-driven particle systems

10.12.2019|14:35 Uhr|Martin Friesen, Hanno Gottschalk, Barbara Rüdiger, Antoine Tordeux

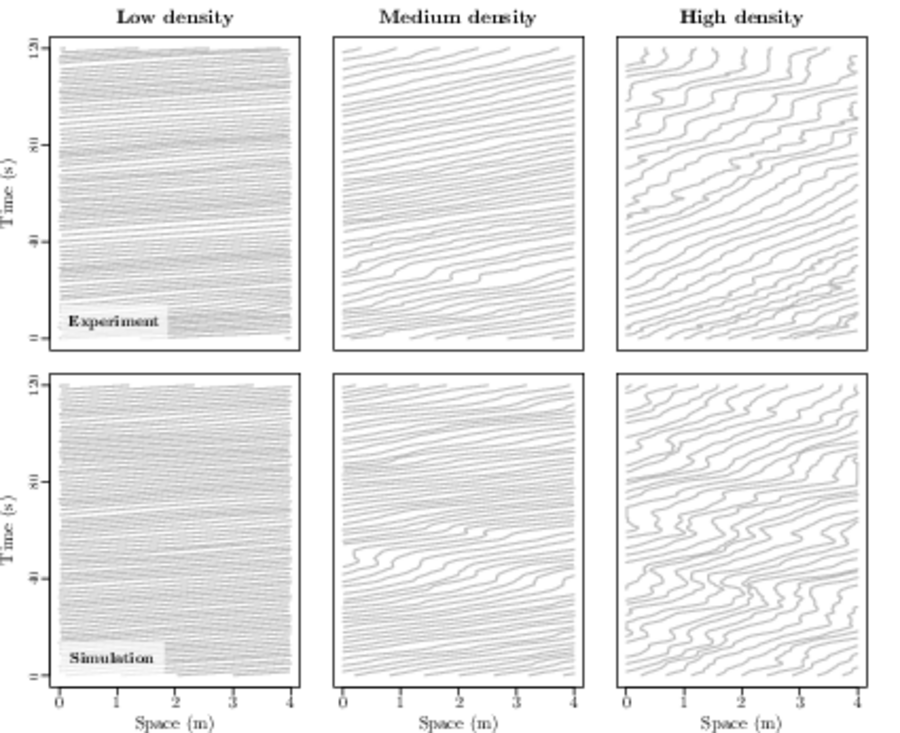
Waves and oscillations are commonly observed in the dynamics of systems self-driven agents such as pedestrians or vehicles. Interestingly, many factors may perturb the stability of homogeneous solutions, leading to the spontaneous formation of waves related as stop-and-go waves or phantom jam in the literature. In this article, we demonstrate that even a minimal additive stochastic noise in stable first-order dynamics can describe stop-and-go phenomena. The noise is not a classic white one, but a colored noise described by a gaussian Ornstein-Uhlenbeck process. It turns out that the joint dynamics of particles and noises forms again a (gaussian) Ornstein-Uhlenbeck process whose characteristics can be explicitly expressed in terms of parameters of the model. We analyze its stability and characterize the presence of waves by calculating the correlation and autocorrelation functions of the distance spacing between the particles. The autocorrelation of the noise induces collective oscillation in the system and spontaneous emergence of waves. While the correlation and autocorrelation functions are complex-valued and difficult to analyze and interpret, we show that these functions become real-valued in the continuum limit when the system size is infinite. Finally, we propose consistent statistical estimations of the model parameters and compare experimental trajectories of single-file pedestrian motions to simulation results of the calibrated stochastic model

arXiv