Pseudospectrum enclosures by discretization

01.05.2020|10:10 Uhr|Lukas Vorberg

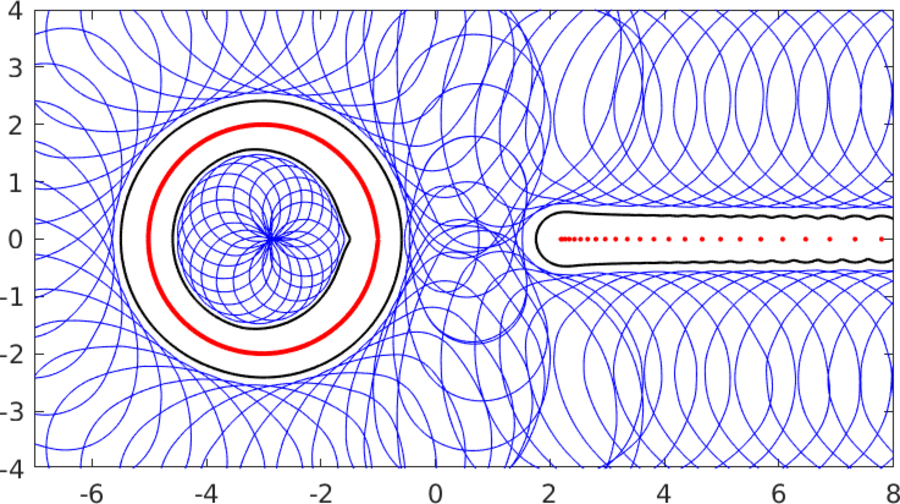
A new method to enclose the pseudospectrum via the numerical range
of the inverse of a matrix or linear operator is presented. The method is
applied to finite-dimensional discretizations of an operator on an infinite-
dimensional Hilbert space, and convergence results for different approxi-
mation schemes are obtained, including finite element methods. We show
that the pseudospectrum of the full operator is contained in an inter-
section of sets which are expressed in terms of the numerical ranges of
shifted inverses of the approximating matrices. The results are illustrated
by means of two examples: the advection-diffusion operator and the Hain-
Lüst operator.

arXiv: http://arxiv.org/abs/2004.12790